[TOC]

快排最引人注目的特点是原地排序（只需要一个很小的辅助栈），且将长度为 N 的数组排序所需的时间和 NlgN 成正比。 而快排的主要缺点是非常脆弱，在实现时必须非常小心才能避免性能低下。

同前述一致：以 C++ 实现,仅针对 vector 进行操作, 并且遵循 C++ 左闭右开的区间标准: [a,b)。

基本算法

快排也是一种分治的排序算法，快排与归并排序是互补的：

• 归并排序将数组分成两个子数组分别排序，再将有序子数组归并以将整个数组排序，其递归调用发生在处理整个数组之前；
• 而快排则是先确定 key 的位置，而后当两个子数组都有序时则整个数组即有序，其递归调用发生在处理整个数组之后。

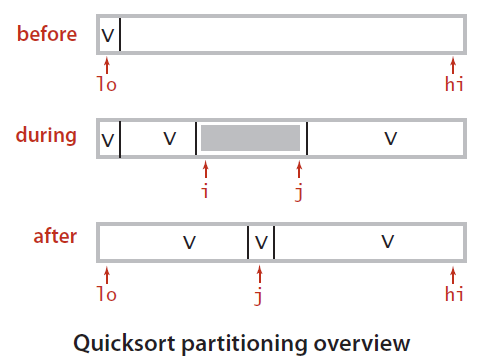
快排的关键在划分，划分过程需要使得数组满足以下三个条件：

• 对于某个 key，a[key] 已经排定；
• [low,key) 中所有元素都不大于 a[key]；
• [key,high) 中所有元素都不小于 a[key]。

据此，快排的基本思想是:

• 选取一个元素作为切分元素 key，然后从数组左端开始向右扫描直到找到一个大于等于它的元素，再从数组右端开始向左扫描直到找到一个小于等于它的元素，而后交换它们的位置;
• 如此继续，就可以保证左指针 left 的左侧元素都不大于 key，右指针 right 的右侧都不小于 key;

• 当左右指针相遇时 （left >= right），将切分元素 key 与左子数组最右元素（也就是 right 最终停下的位置）交换然后返回划分位置 right 即可。

  int Partition(std::vector<T> &vec, int low, int high) {
      int left = low, right = high;
      while (true) {
          // Avoid subscript beging out of range
          while (vec[++left] < vec[low]) if (left == high - 1)break;
          while (vec[low] < vec[--right]) if (right == low)break;
          // Terminate the loop
          if (left >= right)break;
          std::swap(vec[left], vec[right]);
      }
      std::swap(vec[low], vec[right]);
      return right;
  }
  

快排中有若干细节问题值得注意，否则会导致实现错误或者性能下降:

• 越界：这里遵循左闭右开原则 [a,b)，因此左侧不能访问最右元素（右侧可以访问最左元素），否则将会出现越界。本文在内循环中左指针的 break 处理上与右指针有所差异：if (left == high - 1) break。
• 随机性：快排是一个随机化的算法，因此在排序前需将数组随机打乱，在 C++ 中使用 std::random_shuffle 函数对数组进行处理。将数组随机化的原因是希望能够预测并依赖该算法的性能特点，后续本文阐述。
• 循环：当左指针大于或等于右指针时终于划分Partition()中的循环,最后将切分元素 key 放入正确位置： std::swap(vec[key], vec[right])。而事实上， left 和 right 的位置正好一致或相邻。当一侧元素全部小于或大于 key 时，则 left == right，否则 left - 1 == right。

• 递归：当子数组为空或所含元素仅为1个时则无需再处理，在左闭右开区间 [a,b) 中即为 b - a <= 1。否则继续处理，同时为了贯彻左闭右开原则，代码中的递归如下:

  void NormalQuick(std::vector<T> &vec, int low, int high) {
      // Terminate the recursive
  

  ​ if (high - low <= 1){ Insertion(vec, low, high); return; } int nCut = Partition(vec, low, high); // Detail: Use range[low, high) NormalQuick(vec, low, nCut); NormalQuick(vec, nCut + 1, high); ｝

算法改进

1. 切换到插入排序

   和大多数递归排序算法一样，改进快排性能的一个简单办法是在排序小树组时切换到插入排序，从而避免递归调用，并且对于小数组来说快排比插入排序慢。

   经验表明，在大多数情况下 CUTOFF 取值 5~15 能够取得比较好的性能。

   if (high - low <= CUTOFF) {
       Insertion(vec, low, high);
       return;
   }
   

2. 三取样切分

   待补充

3. 熵最优快排——三向切分

   所谓的“熵最优”是指：对于任意分布的输入，最优的基于比较的排序算法平均所需的比较次数与三向切分快排平均所需的比较次数相比，处于常数因子范围之内。当然前提是需要将数组进行随机化。

进一步使用信息论来解释快排性能可参考 Algs4 中的快排章节，Mackayd的Heapsort, Quicksort, and Entropy。刘未鹏的数学之美番外篇：快排为什么那样快也值得一看，浅显易懂。

三向切分快排的运行时间和输入的信息量的 N 倍成正比。对于含有大量重复元素的数组，它将快排的排序时间从线性对数级降低到线性级别。

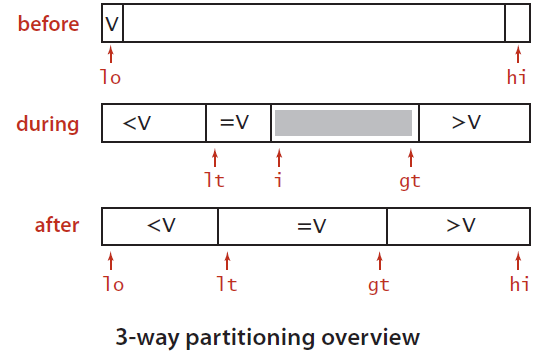
基本想法是将数组切分为三部分，分别对应小于、等于和大于切分元素的数组元素。

Dijkstra 三向切分

Dijkstra 提出的“三向切分快速排序”极为简洁。这里的额外交换用于和切分元素不等的元素。 其从左到右遍历数组一次：

• 维护指针 left 使得 [low, left) 中的元素均小于 key；
• 维护一个指针 right 使得 [right, high) 中的元素均大于 key；
• nMid 使得 [left, nMid) 中的元素均等于 key；
• 余下 [nMid, right) 中的元素尚未排定。

void OptimalQuick(std::vector<T> &vec, int low, int high) {
    if (high - low <= CUTOFF){
        Insertion(vec, low, high);
        return;
    }
    int left = low, nMid = low + 1, right = high - 1;
    T key = vec[low];
    while (nMid <= right)
    {
        if (vec[nMid] < key){
            std::swap(vec[left], vec[nMid]);
            left++; nMid++;
        }
        else if (key < vec[nMid]){
            std::swap(vec[nMid], vec[right]);
            right--;
        }
        else nMid++;
    }
    OptimalQuick(vec, low, nMid);
    OptimalQuick(vec, right + 1, high);
}

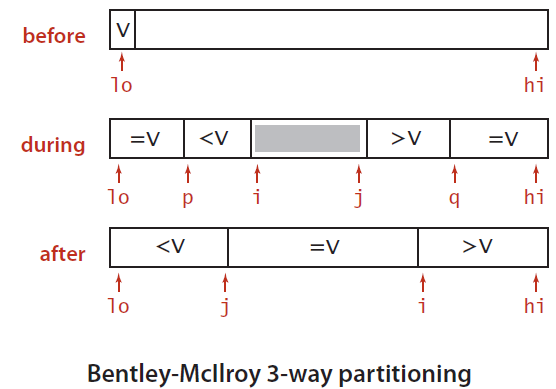
快速三向切分（J.Bently, D.McIlroy)

通过将重复元素置于子数组两端，从而实现一个信息量最优的排序算法。该方法与上述方法是等价的，只是快速三向切分中的额外交换用于和切分元素相等的元素。过程如下：

• 维护指针 p 和 q 使得 vec[low, p) 和 vec[q, high) 中的元素都和 key 相等;
• 维护指针 i 和 j 使得 vec[p, i) 中的元素小于 key ，vec[j, q) 中的元素大于 key;
• 在切分循环结束后将和 key 相等的元素交换到正确的位置上。

void QuickX(std::vector<T> &vec, int low, int high) {
    if (high - low <= CUTOFF){
        Insertion(vec, low, high);
        return;
    }

    int p = low, q = high, i = low, j = high;
    T key = vec[low];
    while (true){
        while (vec[++i] < key)if (i == high - 1)break;
        while (key < vec[--j])if (j == low)break;
        if (i == j && key == vec[i]){
            std::swap(vec[++p], vec[i]);
        }
        if (i >= j)break;
        std::swap(vec[i], vec[j]);
        // exchange only when equal to key
        if(vec[i] == key)std::swap(vec[++p], vec[i]);
        if(vec[j] == key)std::swap(vec[--q], vec[j]);
    }
    // exchange to right position
    i = j + 1;
    while (p >= low)std::swap(vec[p--], vec[j--]);
    while (q < high)std::swap(vec[q++], vec[i++]);
    // recursive
    QuickX(vec, low, j + 1);
    QuickX(vec, i, high);
}   

---

Reference：

Algs4

Heapsort, Quicksort, and Entropy

数学之美番外篇：快排为什么那样快